Iterierte Funktionensysteme

Herleitung der Werte für das Dürerfünfeck

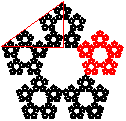
Die Seitenlänge des großen (schwarzen) Fünfecks sei 1, die des kleinen (roten) Fünfecks sei k. Dann setzt sich die Seitenlänge des großen Fünfecks wie folgt zusammen: 1 = k + x + k (siehe Abb. 3). Dabei ist x die Basis des Keils, der sich zwischen zwei benachbarten kleinen Fünfecken befindet. Dieser Keil ist ein gleichschenkliges Dreieck mit der Schenkellänge k. Da dieses Dreieck und drei kleine Fünfecke (Innenwinkel 540° : 5 = 108°) einen Punkt gemeinsam haben, gilt für den Winkel an der Spitze γ=360°-3·108°=36°. Also gilt: sin 18° = ½·x/k, also x = 2k·sin 18°. Wegen sin 18° = ¼·( - 1) gilt x = 2k·¼·( - 1) = ½k·( - 1). Damit folgt aus dem Ansatz: 1 = k + ½k·( - 1) + k. Stellt man diese Gleichung nach k um, erhält man den Streckfaktor k = ½·(3 - ).

	Abbildung 1	Abbildung 2	Abbildung 3	Abbildung 4	Abbildung 5
	←→↔←→
	k   x   k
	dx = 0	dx = ½·( - 1)	dx = ¼·( + 1)	dx = ¼·( - 1)	dx = ¼·( - 3)
	dy = 0	dy = 0	dy = ¼·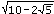	dy = ¼·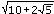	dy = ¼·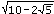

Abb. 2: Das zweite kleine Fünfeck ist gegenüber dem ersten Fünfeck um dx = 1-k nach rechts verschoben. Also gilt:
dx = 1 - ½·(3 - ) = 1 - ½·3 + ½· = ½· - ½ = ½·( - 1).

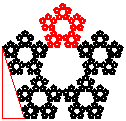
Abb. 3: Das dritte kleine Fünfeck ist gegenüber dem ersten Fünfeck um dx = 1-½·k nach rechts verschoben. Also gilt:
dx = 1 - ¼·(3 - ) = 1 - ¼·3 + ¼· = ¼ + ¼· = ¼·( + 1).
Außerdem ist es um die Höhe dy (kürzere Kathete im rot hervorgehobenen Dreieck) des Fünfecks nach oben verschoben.
Daraus folgt: sin 36° = dy/1. Da sin 36° = ¼·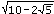 ist, gilt dy = ¼·.

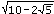Abb. 4: Das vierte kleine Fünfeck ist gegenüber dem ersten Fünfeck um dx = ½-½·k nach rechts verschoben. Also gilt:
dx = ½ - ¼·(3-) = ½ - ¼·3 + ¼· = -¼ + ¼· = ¼·( - 1).
Außerdem ist es um die Höhe dy (lange Kathete im rot hervorgehobenen Dreieck) nach oben verschoben.
Daraus folgt: cos 18° = dy/1. Da cos 18° = ¼·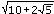 ist, gilt dy = ¼·.

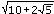Abb. 5: Das fünfte kleine Fünfeck ist gegenüber dem ersten Fünfeck um dx = ½·k nach links verschoben. Also gilt:
dx = 0 - ¼·(3 - ) = -¼·(3 - ) = ¼·( - 3). Die Verschiebung nach oben ist dieselbe wie in Abbildung 3.

zurück zum Dürerfünfeck