Hilfe: Glossar

Attraktor

Ein Attraktor eines dynamischen Systems ist die sich zeitlich nicht ändernde (invariante) oder sich dieser asymptotisch nähernde Untermenge eines Zustandsraumes, die unter der Dynamik dieses Systems nicht mehr verlassen wird. Die Menge aller Punkte des Zustandsraumes, die unter der Dynamik demselben Attraktor zustreben, heißt Attraktionsgebiet dieses Attraktors.

affine Abbildung

Eine affine Abbildung ist eine Abbildung, bei der parallele Linien der Originalfigur parallel bleiben, d.h. auch in der Bildfigur noch parallel zueinander verlaufen. Also sind zentrische Streckung, Parallelstreckung, Verschiebung, Spiegelung, Scherung und Drehung bzw. deren Verkettung affine Abbildungen.

Dimension

topologische Dimension D_T

Strecken und Streckenzüge (z. B. die Kochkurve) besitzen die topologische Dimension 1.
Ebene Flächen (z. B. das Rechteck) und gekrümmte Flächen (z.B. der Kegel-Mantel) besitzen die topologische Dimension 2.
Körper (z.B. der Zylinder) besitzen die topologische Dimension 3.

fraktale Dimension D

Der Begriff soll am Beispiel der Kochkurve erläutert werden:

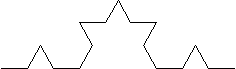
Die Kochkurve der Breite b kann in N = 4 verkleinerte Teile der Länge 1/3·b zerlegt werden. Man sagt, der Verkürzungsfaktor r beträgt 1/3.

Die fraktale Dimension ist diejenige reelle Zahl D, für die gilt N· r^D = 1.

Daraus folgt D = ln(N) / ln(1/r). Für die Kochkurve gilt demnach 4· (1/3)^D = 1, sie hat die fraktale Dimension D = ln(4) / ln(3) ≈ 1,2618.

Dithering

Das Dithering (englisch »to dither«: schwanken, zittern) ist eine Technik der Computergrafik, um bei Bildern mit geringer Farbtiefe die Illusion einer größeren Farbtiefe zu erzeugen. Bei einem so bearbeitetem Bild werden die fehlenden Farben durch eine bestimmte Pixel-Anordnung aus verfügbaren Farben nachgebildet und dadurch harte Übergänge zwischen den Farben vermieden. Das menschliche Auge nimmt das Dithering als Mischung der einzelnen Farben wahr. Dithering wird auch als Fehlerdiffusion oder Farbrasterung bezeichnet.

Fehlerdiffusions-Methode

Die Fehlerdiffusions-Methode ist ein weit verbreitetes Dithering-Verfahren. Das Wort Fehler in der Bezeichnung bezieht sich auf den kumulativen Unterschied zwischen den tatsächlichen Farbwerten der dargestellten Pixel und den Farbwerten, welche die Pixel bei der Darstellung in der korrekten Farbe aufwiesen. Durch eine Verminderung dieses Fehlers kann diese spezielle Dithering-Methode eine höhere Bildqualität erzeugen als dies andere Methoden ohne Fehlerkorrektur vermögen.

Der eigentliche Prozess beginnt mit dem ersten Pixel des Bildes (der linken, oberen Ecke). Der Algorithmus sucht nun nach der Palettenfarbe, die der Originalfarbe am nächsten kommt, und vergleicht die numerischen Werte beider Farben. Die Differenz der beiden Werte wird als Anfangsfehler gespeichert und die Palettenfarbe dem Pixel zugeordnet. Der Prozess geht nun zu dem zweiten Pixel über, wiederholt den Farbvergleich und ordnet dem zweiten Pixel die Palettenfarbe zu, deren Farbwert der Summe aus dem Originalwert des zweiten Pixels und dem Fehlerwert des ersten Pixels am nächsten kommt. Die Differenz zwischen dem neuen Farbwert und dieser Summe wird als der neue Fehlerwert gespeichert. Der Farbwert für den dritten Pixel wird nun mit Hilfe der Methode festgelegt, die zur Darstellung des zweiten Pixels verwendet wurde. Der Algorithmus berechnet auf diese Weise die Farbwerte für alle restlichen Pixel des Bildes. Der Fehlerwert wird am Ende jeder Reihe verworfen.

Die einzelnen Farben verlaufen aufgrund des Dithering von links nach rechts immer mehr. Dies ist durch den Algorithmus bedingt, da sich der Fehler von links nach rechts fortpflanzt. Das Verlaufen der Farben wird besonders deutlich bei Bildern mit harten vertikalen Kanten, da diese Kanten durch das Verlaufen »aufgeweicht« werden.

Fraktal

Ein Fraktal ist eine Menge, deren fraktale Dimension D die topologische Dimension D_T übersteigt.

Ein Quadrat ist demnach – im Gegensatz zur Kochkurve – kein Fraktal: Wird es in N = 4 gleiche Teile zerlegt, entstehen kleinere Quadrate mit dem Verkürzungsfaktor r = 1/2. Demnach hat es nicht nur die topologische Dimension D_T = 2, sondern auch die fraktale Dimension D = ln (4) / ln (2) = 2.

Gaußsche Zahlenebene
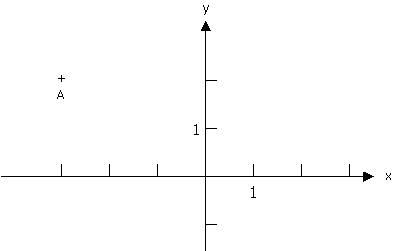Die Gaußsche Zahlenebene (komplexe Zahlenebene) wird durch die reelle Achse (x-Achse) und die imaginäre Achse (y-Achse) gebildet. Jeder Punkt der Ebene repräsentiert eine komplexe Zahl. Der Punkt A stellt die komplexe Zahl -3 + 2 · i dar.

Iterationstiefe

Jedes Fraktal beruht auf einer bestimmten Berechnungsvorschrift, die für jeden einzelnen Bildpunkt wiederholt zu durchlaufen ist. Die Anzahl dieser Iterationen (Synonym für Wiederholungen) nennt man Iterationstiefe.

komplexe Zahl

Jede komplexe Zahl c hat die Form a + b · i. a heißt Realteil und b Imaginärteil. So hat z. B. die komplexe Zahl c = 5 + 2 · i den Realteil 5 und den Imaginärteil 2. Bei der Zahl c = 3 ist der Imaginärteil Null, bei c = 2 · i der Realteil Null.

Die Notwendigkeit komplexer Zahlen ergibt sich aus der Tatsache, dass das Radizieren im Bereich der reellen Zahlen nicht uneingeschränkt ausführbar ist: So sind im Bereich der reellen Zahlen z. B. 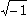und 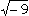nicht definiert.

Mit der Festlegung der imaginären Einheit i und der Definition i² = (-1) wird diese Einschränkung aufgehoben. Im Bereich der komplexen Zahlen gilt: 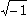= = 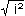i und 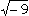= = 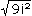3i.

Newton-Verfahren

Um die Nullstelle einer differenzierbaren Funktion zu ermitteln, bestimmt man grafisch eine Näherungslösung x und verwendet diese als Startwert der Iterationsvorschrift x := x - f(x) / f´(x).

Beispiel: Die Nullstelle der Funktion f(x) = x³ - x + 1 im Intervall [-2; 0] soll ermittelt werden:
Wegen f´(x) = 3x² - 1 lautet die Iterationsvorschrift: x := x - (x³ - x + 1) / (3x² - 1) bzw. umgeformt x := (2x³ - 1) / (3x² -1).

Startet man das Iterationsverfahren mit x(0) = -1, dann erhält man nacheinander x(1) = -1,5; x(2) = -1,3478; x(3) = -1,3252; x(4) = -1,3247 usw. Also ist die gesuchte Nullstelle auf zwei Dezimalen genau -1,32.

Parallelstreckung

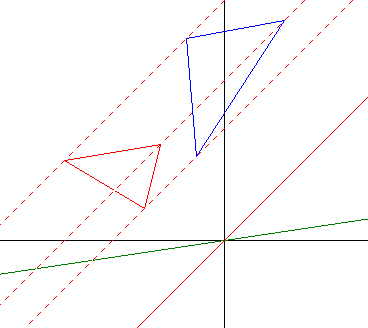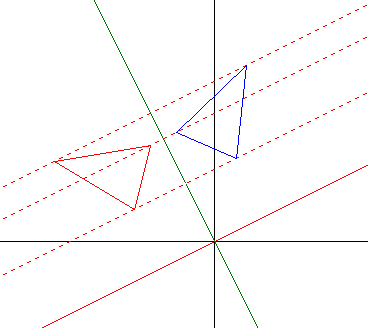Streckachse y = 0,15x Richtungsachse y = x Streckfaktor k = 2	Streckachse y = -2x Richtungsachse y = 0,5x Streckfaktor k = -1

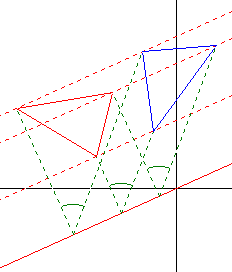
Für k = -1 liegt eine sogenannte Schrägspiegelung vor. Stehen wie in der rechten Abbildung zudem Streck- und Richtungsachse senkrecht aufeinander, handelt es sich um eine Achsenspiegelung.

Pixel

Pixel ist ein Kunstwort, das aus den englischen Begriffen Picture und element gebildet wurde. Dabei ist das c zu einem x »mutiert«. Es heißt also übersetzt Bildpunkt. Siehe auch Grafikformate!

Satz von Moivre

Jede komplexe Zahl z = a + b · i lässt sich auch in der Form z = r (cos α + i sin α) mit r² = a² + b² und α = arctan (b/a) darstellen. Der französische Mathematiker Abraham de Moivre bewies den nach ihm benannten Satz:
Für jede komplexe Zahl z gilt : zⁿ = rⁿ (cos nα + i sin nα).
Wendet man diese Erkenntnis auf das Newtonverfahren an, dann erhält man für f(z) = zⁿ - 1 folgende Iterationsvorschrift:

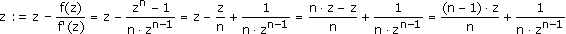
Mit der Vereinbarung m = n - 1 wird daraus


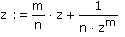
und unter Verwendung des Satzes von Moivre:













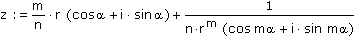
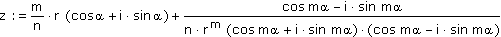
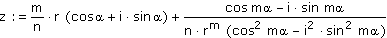
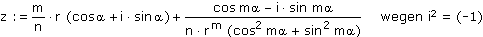
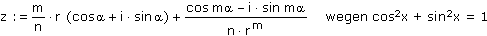
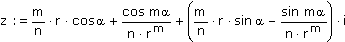
Die so gewonnene Formel wird bei der Programmierung der Newton-Fraktale verwendet.

Scherung

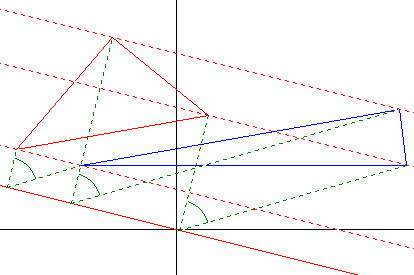Scherungsachse y = 0,45 x Scherungswinkel 45°	Scherungsachse y = -0,25 x Scherungswinkel 60°

Selbstähnlichkeit

strenge Selbstähnlichkeit

Ein Objekt heißt selbstähnlich, wenn es bei der Teilung der Kanten in r gleiche Abschnitte in N gleiche Teile zerfällt. In diesem Fall genügt die fraktale Dimension D der Bedingung N · r^D=1 und lässt sich schreiben als D = ln (N) / ln (1/r).

Selbstähnlichkeit im weiteren Sinne

Das Grundmotiv des Fraktals besteht aus N Strecken der Länge 1/r und M Strecken der Länge 1/s. In diesem Fall genügt die fraktale Dimension D der Bedingung N · r^D + M · s^D = 1. Diese Gleichung lässt sich im allgemeinen nur numerisch lösen.