Anwendungen zu Fraktalen

Das Räuber-Beute-Modell von Lotka und Volterra

Das bekannteste Modell eines Räuber-Beute-Systems stammt von dem italienischen Mathematiker und Physiker Vito Volterra und dem österreichisch-amerikanischen Mathematiker Alfred James Lotka, welche die nachfolgenden Gleichungen 1925 und 1926 unabhängig voneinander formuliert hatten. Mit Hilfe ihres Modells konnte die dramatische Abnahme des Sardinen-Fischfangs nach dem ersten Weltkrieg erklärt werden. Ist x die Beute- und y die Räuber-Population, so gelten die sogenannten Lotka-Volterra-Gleichungen:

dx                     dy
—— = ax - bxy          —— = -cy + dxy
dt                     dt

Dabei sind a, b, c und d positive Konstanten:

• a : Geburtenrate der Beute
• b : Abnahme der Beute
• c : Geburtenrate des Räubers
• d : Zuwachs des Räubers

Wenn die Ableitungen dieser Differentialgleichungen Null sind, erhält man den Fixpunkt:
ax - bxy = 0 → ax = bxy → a = by → y = a/b
dxy - cy = 0 → cy = dxy → c = dx → x = c/d
Also ist der Attraktor stets der Punkt (c/d; a/b).

In der von Lotka und Volterra untersuchten Situation waren x(t) bzw. y(t) die Bestände von Sardinen und Haien im Mittelmeer. Die Richtigkeit ihrer Regeln wurde auch durch die Statistik der Hudson Bay Company zwischen 1845 und 1935 hinsichtlich der eingelieferten Felle von Luchsen und Schneehasen belegt.

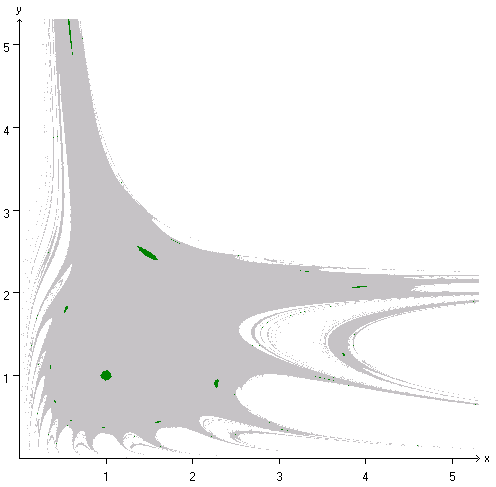Das Bild zeigt das Attraktionsgebiet des Räuber-Beute-Systems für a = b = c = d = 1. In diesem Fall ist der Attraktor der Punkt (1; 1). Alle Punkte (z.B. x = 1.5 und y = 2.5), die nach 100 Iterationen zu diesem Attraktor führen, sind grün gefärbt. Das bedeutet, alle diese Situationen führen zu stabilen Populationen sowohl der Beute- als auch der Raubtiere. Die grau gefärbten Punkte stellen Situationen dar, bei denen nach 100 Iterationen weder x noch y größer als 10 sind. Alle anderen Fälle (die weiß gefärbten Punkte) führen in absehbarer Zeit entweder bei der Räuber- oder bei der Beutepopulation zu einem starken Anwachsen.

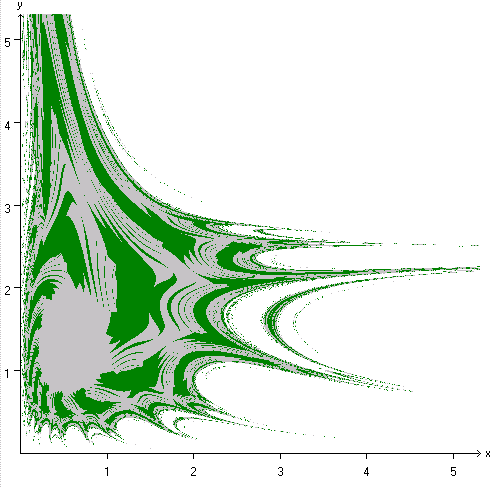Für a = 1.24; c = 0.5 und b = d = 1 erhält man ein völlig anderes Attraktionsgebiet. Hier ist der Attraktor der Punkt (0.5; 1.24). Ein Programm für die Erstellung solcher Attraktionsgebiete finden Sie hier.