Fraktale
Julia-Mengen
Auch zur Berechnung von Julia-Mengen beginnt man in der linken oberen Ecke des Bildausschnitts (z. B. z(0) = -2,4 + 1,75i), testet spaltenweise das Verhalten aller Pixel nach der Vorschrift z := z² + c aus und färbt sie je nach Verlassen des Kreises ein – bis man den Bildpunkt in der rechten unteren Ecke (z. B. z(0) = 2,4 -1,75i) erreicht hat.
Der einzige Unterschied zur Mandelbrot-Menge besteht im Wert c. Während bei der Mandelbrot-Menge für jeden einzelnen Bildpunkt dessen Koordinaten als c gewählt wurden, verwendet man bei einer Julia-Menge stets denselben Wert c, im Beispiel c = -0,80 + 0,15i. Würde man hingegen für jeden Bildpunkt den Wert c = -1 verwenden, erhielte man eine andere Julia-Menge, nämlich den sogenannten »San-Marco-Drachen« – benannt nach dem ähnlich aussehenden Umriss der Markuskirche in Venedig (Basilica di San Marco). Da man den festen Wert c frei wählen kann, gibt es unendlich viele Julia-Mengen.
| Definition Eine Juliamenge Jc ist die Menge aller Punkte z0, für die die Iteration zn := zn-1² + c (c = konstant, Startwert z0 : Bildpunkt) nicht gegen Unendlich strebt:  |
 |
Drachen (Gaston Julia) z := z² + c c (real) := -0,80 c (imag) := 0,15 Download von julia.pas |
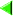 Mandelbrot-Menge Mandelbrot-Menge |
Newton-Fraktale  |

