Fraktale

Die Mandelbrot-Menge (1980)

Der Bildschirm wird als Gaußsche Zahlenebene und jeder Bildpunkt (Pixel) des Bildschirms als Startwert c einer Zahlenfolge aufgefasst. Dabei ist c eine komplexe Zahl und repräsentiert einen Punkt der Ebene. Die Zahlenfolge wird nach der Vorschrift z := z² + c gebildet.

Man denkt sich einen Kreis mit dem Radius 3 LE (Längeneinheiten) um den Koordinatenursprung. Verlässt ein Wert z den gedachten Kreis, dann wird der Punkt c gefärbt: Wird der Kreis bereits nach dem ersten Berechnungsschritt verlassen, wird er blau gefärbt, nach dem zweiten grün, nach dem dritten türkis, nach dem vierten rot usw. Verlässt hingegen z den Kreis auch nach dem 25. Schritt (maximale Iterationstiefe 25) nicht, dann bleibt der Punkt c schwarz.

Man beginnt in der linken oberen Ecke des Bildausschnitts (z.B. c = -2,4 + 1,75i), testet spaltenweise das Verhalten aller Pixel aus und färbt sie je nach Verlassen des Kreises ein – bis man den Bildpunkt in der rechten unteren Ecke (z. B. c = 1,6 -1,75i) erreicht hat. Bei einer Auflösung von 800 × 600 muss auf diese Art und Weise immerhin von 480.000 Bildpunkten die Farbe berechnet werden! Das ist der Grund, weshalb selbst schnelle Rechner mehrere Sekunden oder gar Minuten für die Berechnung eines Fraktals benötigen – je nachdem, welches Fraktal, welcher Bildausschnitt und welche maximale Iterationstiefe verwendet wird.

Definition Die Mandelbrotmenge M  ist die Menge aller Punkte c, für die die Iteration zn := zn-1² + c (c : Bildpunkt, Startwert z0 = 0) nicht gegen Unendlich strebt: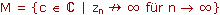

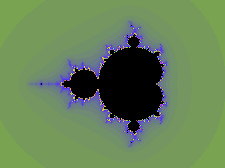Das Apfelmännchen (Benoît Mandelbrot) z := z² + c c (real) := x-Wert des Pixels c (imag) := y-Wert des Pixels Download von mandel.pas

Bildergalerie

Julia-Mengen